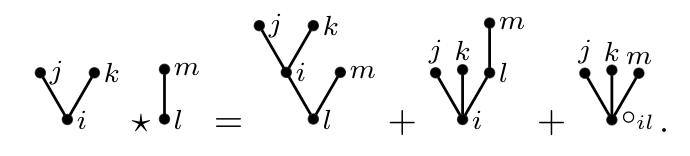Linear-Quadratic McKean-Vlasov Stochastic Differential Games
Published in Modeling, Stochastic Control, Optimization, and Applications. The IMA Volumes in Mathematics and its Applications, vol 164. Springer, Cham, with Huyên Pham, 2019
Recommended citation: https://arxiv.org/abs/1812.00632
Co-authors
Abstract
We consider a multi-player stochastic differential game with linear McKean-Vlasov dynamics and quadratic cost functional depending on the variance and mean of the state and control actions of the players in open-loop form. Finite and infinite horizon problems with possibly some random coefficients as well as common noise are addressed. We propose a simple direct approach based on weak martingale optimality principle together with a fixed point argument in the space of controls for solving this game problem. The Nash equilibria are characterized in terms of systems of Riccati ordinary differential equations and linear mean-field backward stochastic differential equations: existence and uniqueness conditions are provided for such systems. Finally, we illustrate our results on a toy example.