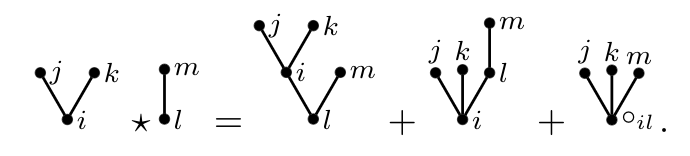Linear-quadratic stochastic delayed control and deep learning resolution

Co-authors

• William Lefebvre

Abstract

We consider a class of stochastic control problems with a delayed control, both in drift and diffusion, of the type \(dXt = α_{t−d}(bdt + σdWt)\). We provide a new characterization of the solution in terms of a set of Riccati partial differential equations. Existence and uniqueness are obtained under a sufficient condition expressed directly as a relation between the horizon \(T\) and the quantity \(d(b/σ)^2\). Furthermore, a deep learning scheme is designed and used to illustrate the effect of delay on the Markowitz portfolio allocation problem with execution delay.