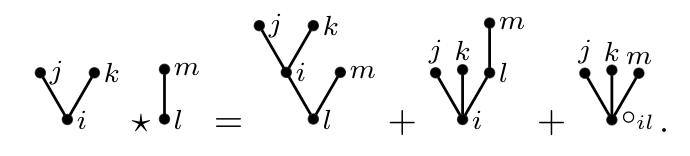Stochastic maximum principle for optimal control problem of non exchangeable mean field systems
Published:
Recommended citation: https://arxiv.org/abs/2506.05595
Co-authors
Abstract
We study the Pontryagin maximum principle for a class of optimal control problems arising in non exchangeable mean field systems, where agents interact through heterogeneous and asymmetric couplings. Our analysis leads to a collection of forward-backward stochastic differential equations (FBSDE) of non exchangeable mean field type. Under suitable assumptions, we establish the existence and uniqueness of solution to this system. As an illustration, we consider the linear-quadratic case, where the optimal control is characterized by an infinite dimensional system of Riccati equations. We also provide an application to a systemic risk model involving heterogeneous banks.