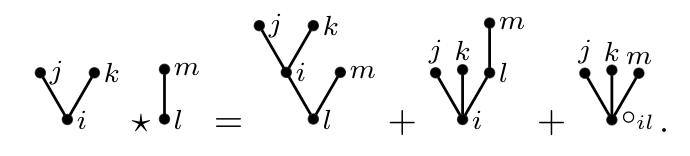Optimal control of heterogeneous mean-field stochastic differential equations with common noise and applications to financial models

Co-authors

• Filippo de Feo

Abstract

Optimal control of heterogeneous mean-field stochastic differential equations with common noise has not been addressed in the literature. In this work, we initiate the study of such models. We formulate the problem within a linear–quadratic framework, a particularly important class in control theory, typically renowned for its analytical tractability and broad range of applications. We derive a novel system of backward stochastic Riccati equations on infinite-dimensional Hilbert spaces. As this system is not covered by standard theory, we establish existence and uniqueness of solutions. We explicitly characterize the optimal control in term of the solution of such system. We apply these results to solve two problems arising in mathematical finance: optimal trading with heterogeneous market participants and systemic risk in networks of heterogeneous banks.